プログラミングオンライン講座「プログラミングアート~コンピュータで作れるふしぎなもよう~」が実施されました。
福井県内8校合計300名弱の小学校5,6年生の児童にプログラミングを楽しんでいただきました。 今回のテーマは「フラクタル図形」です。 算数で習った図形の知識を活かして,ふしぎなもようを描いていきます。 本日の講師は,福井大学教育学部技術科の4年生です。大学にあるICTルームから電子黒板を使って分かりやすく説明してくれました

正三角形を描くには何度回転させればよいでしょうか?
算数の授業を思い出して考えます。

描いた三角形はちょっとずらしてまた三角形を描いていきます。
色んなずらし方で様々なもように変わります。

講座中に設けたフリータイムでは教わったことを元に,児童たちにオリジナルのもようを考えてもらいました。
みんな集中して取り組んでくれています。
作ったもようは,学校を超えて作品鑑賞です。星形のような素敵なもようが描けていますね。
素敵な作品を紹介します。
優秀作品の紹介(学生賞)
学生からのコメント
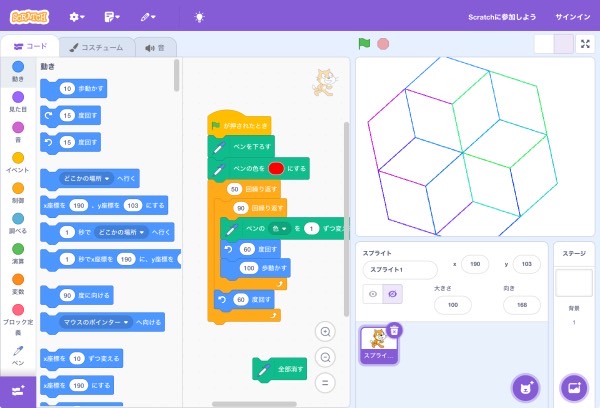
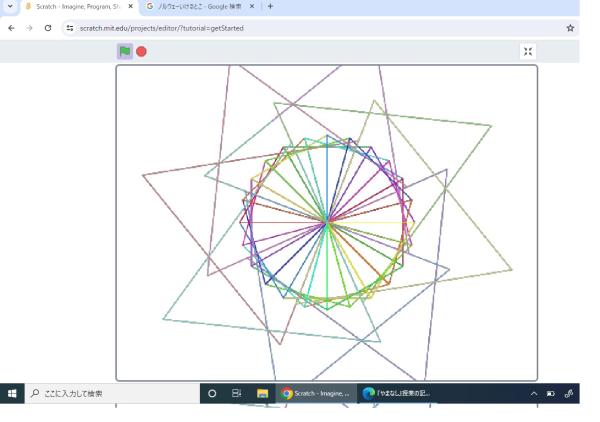
立体的に見える不思議な作品です。ですが、プログラム自体は正六角形を60度ずつ回転させたシンプルなものです。それを色の変化で立体的に表現している所がとても素敵だと思いました。図形の外枠が正六角形になっている点もプラス評価です!
学生からのコメント
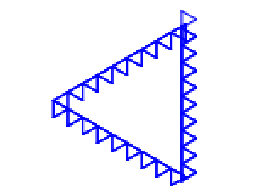
大きさの異なる三角形をそれぞれ回転させた不規則に見えて規則的な不思議な図形です。大きい三角形は描き始めが頂点からではなく、辺の途中から始まっている所がポイントであり、その長さの比をあえて1:1にしないという工夫がこの図形の魅力であると考えます。
学生からのコメント
図形の回転以外の方法でフラクタルを作ってみようという発想と、三角形を用いて三角形を描くという発想がとてもおもしろいなと感じました。コッホ雪片※のようにも捉えることができ、フラクタルの数学的な意味を見る上でも、辺を図形で複雑に置き換えていくことはいいなと思います。

※コッホ雪片
数学で扱われる有名なフラクタル図形,雪の結晶のような形をしています。
優秀作品の紹介(小林賞)
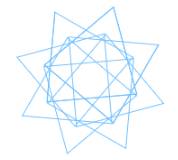
小林からのコメント
三角形などの図形でなくても,規則正しく
・線を引く
・角度を変える
を繰り返すだけでも実はきれいな形になる時があります。
コンピュータだからこそ描ける模様ですね。とてもきれいに描けています。
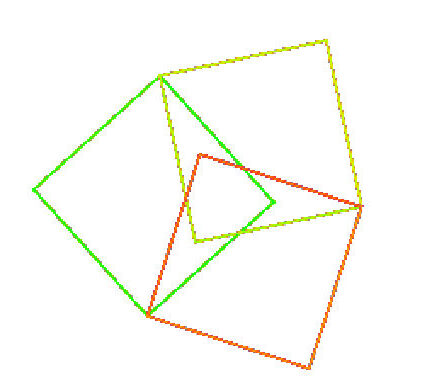
小林からのコメント
シンプルですが奥が深い作品です。
四角形を3回書いただけですがきれいに1周しています。どのようなプログラムにすればこの図形が描けるか想像できますか?
やってみると意外と悩んでしまう不思議なもようです。
講座の感想,Q&A
児童の感想(とてもよかったと感じた理由) ・描きたい図形が書けた時も嬉しいけれど、思ってもいない新たな不思議な図形ができることが嬉しいからです。 ・三角形や四角形などを繰り返し違う場所に並べることで色々な面白い図形ができて面白かったから ・何度回したらこの形になるかを考えていろんな形を作れて楽しかったです。最初はうまく動かせなかったけど、慣れてきて動かせるようになって楽しかったです。 ・自分で好きに変換できて、正解がない感じで楽しかったからです。 先生の感想 ・丁寧に操作しながら教えていただいて、誰1人取り残されることなくできていたので、ありがたかったです。 ・スキルとして教えていただける時間だけでなく、自由に作れる時間があり子供たちも発見する喜びを感じながら生き生きと活動していました。ありがとうございました。 ・プログラミングに初めて触れる児童がほとんどでしたが、1から丁寧に教えていただきわかりやすかったです。他の学校の子の作品も見ることができたのも、よかったです。 ・初めにわかりやすく丁寧に教えてくださったので、子どもたちは戸惑いなく取り組むことができました。 ・トライ&エラーで何度もプログラミングしている様子はまさに主体的な活動でした。 児童からの質問 Q.ペンをおろすをいれてないのになぜかかけたのですがなぜですか。

A.ペンを下ろすの他に「ペンを上げる」というブロックがあります。一度ペンを下ろしたら,下がったままなので,どこかで「ペンを上げる」というブロックを入れてみてください。
Q.他のものの詳しい作り方の例(いつでも見れるもの)を教えて欲しかった
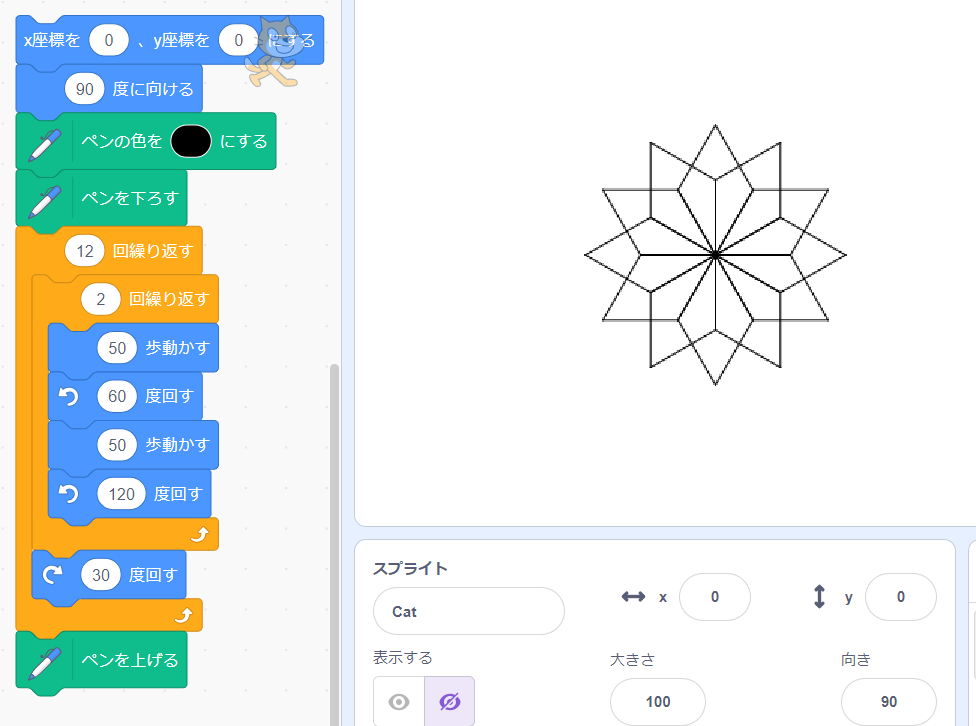
Q.福井大学が書いた図形を知りたい
A.では1つ応用問題です。以下の図形を描いてみてください。ひし形を回転させて描いています。
一気にプログラムを作るのではなく,
・まずはひし形をきれいに描いてみる。
・ひし形が描けたら,ひし形をずらして再度ひし形を描いてちょうど一周させる
と分けてプログラミングしてみましょう。
何度で回すのを何回繰り返せばきれいに一周になるか,を考えるのがポイントです。
分からなければ左側のプログラムも見てみてください。